一、SGC [2019]

《Simplifying Graph Convolutional Networks》

1. 图卷积网络（Graph Convolutional Network: GCN ）及其变体已备受关注，并成为学习 graph representations 的实际标准方法。GCN 主要从近期的深度学习方法中汲取灵感，因此可能继承了不必要的复杂性和冗余计算。在本文中，我们通过依次移除非线性激活函数、以及合并连续层之间的权重矩阵来减少这种过度复杂性。我们对所得的线性模型进行了理论分析，结果表明它对应于一个固定的低通滤波器（low-pass filter），其后接一个线性分类器。值得注意的是，我们的实验评估表明，这些简化在许多下游应用中不会对准确性产生负面影响。此外，所得模型可扩展到更大的数据集，具有自然的可解释性，并且与 FastGCN 相比，速度提升可达两个数量级。

2. 图卷积网络（Graph Convolutional Network: GCN ）是图上卷积神经网络（Convolutional Neural Network: CNN）的一种高效变体。GCN 堆叠了多层的学习好的一阶谱滤波器（spectral filters），随后应用非线性激活函数来学习 graph representations。最近，GCN 及其后续变体在各个应用领域都取得了 SOTA 的结果，包括但不限于引文网络（citation networks）、社交网络（social networks）、应用化学（applied chemistry）、自然语言处理、以及计算机视觉。

   从历史上看，机器学习算法的发展遵循着从初始的简单性到需求驱动的复杂性（need-driven complexity）这一清晰趋势。例如，线性感知机（linear Perceptron）的局限性推动了更复杂但表达能力更强的神经网络（或多层感知机，即 MLP）的发展。类似地，简单的预定义的线性 image filters 最终演变为具有 learned convolutional kernels 的非线性 CNN。由于额外的算法复杂性往往会使理论分析复杂化并模糊 understanding，因此通常仅仅在 simpler methods 表现不佳的 applications 中引入复杂的算法。可以说，现实世界应用中的大多数分类器仍然是线性的（通常是 logistic regression），它们易于优化且易于解释。

   然而，可能因为 GCN 是在神经网络近期“复兴”之后提出的，所以它们往往是这一趋势的罕见例外。GCN 建立在多层神经网络的基础上，从未是 simpler（insufficient ）的线性对应物的扩展。

   在本文中，我们观察到 GCN 从其深度学习的沿袭中继承了相当大的复杂性，这对于要求较低的应用来说可能是繁重且不必要的。受历史上明显缺乏 simpler 前身的启发，我们旨在推导如果采用更“传统”的路径，本可以先于 GCN 出现的最简单线性模型。我们通过反复移除 GCN 层之间的非线性激活函数，并将所得函数合并为单个线性变换，来减少 GCN 的过度复杂性。我们通过实验表明，最终的线性模型在各种任务上表现出与 GCN 相当甚至更优的性能，同时计算效率更高，拟合的参数显著更少。我们将这种简化的线性模型称为 Simple Graph Convolution: SGC。

   与非线性模型相比，SGC 具有直观的可解释性，我们从 graph convolution 的角度提供了理论分析。值得注意的是，SGC 中的特征提取对应于应用于每个特征维度的单个 fixed filter 。《Semi-supervised classification with graph convolutional networks》 通过实验观察到 “重新归一化技巧”（renormalization trick），即向图中添加自环，提高了准确性，我们证明该方法有效地缩小了图的谱域（graph spectral domain），当应用于 SGC 时会产生低通型滤波器（low-pass-type filter）。至关重要的是，这种滤波操作会在整个图中产生局部平滑的特征（《Spectral networks and locally connected networks on graphs》）。

   通过对引文网络和社交网络的节点分类基准数据集的实证评估，我们表明 SGC 取得了与 GCN 和其他 SOTA 的图神经网络相当的性能。然而，它的速度明显更快，在我们评估的最大数据集（ Reddit ）上，甚至比 FastGCN 快达两个数量级。最后，我们证明 SGC 的有效性可推广到广泛的下游任务。特别是，在文本分类、用户地理定位（user geolocation ）、关系抽取、以及 zero-shot 图像分类任务中，SGC 即使不超越 GCN-based 的方法，也与之相当。代码可在 Github 上获取（https://github.com/Tiiiger/SGC）。

1.1 Simple Graph Convolution

1. 我们遵循 《Semi-supervised classification with graph convolutional networks》 在节点分类的上下文中介绍 GCN（以及随后的 SGC）。在这里，GCN 将具有一些 labeled nodes 的 graph 作为输入，并为所有 graph nodes 生成 label predictions。我们正式将这样的 graph 定义为 $\mathcal{G}=(\mathcal{V},\mathbf{A})$$\mathcal G=(\mathcal V, \mathbf A)$ ，其中：

   • $\mathcal{V}$$\mathcal V$ 表示由节点 $\{v_1,\cdots ,v_n\}$$\{v_{1}, \cdots, v_{n}\}$ 组成的顶点集合。

   • $\mathbf{A}\in {\mathbb{R}}^{n\times n}$$\mathbf A \in \mathbb{R}^{n ×n}$ 是对称的（通常是稀疏的）邻接矩阵，其中 $a_{ij}$$a_{i j}$ 表示节点 $v_i$$v_{i}$ 和 $v_j$$v_{j}$ 之间的边的权重。缺失的边用 $a_{ij}=0$$a_{i j}=0$ 表示。

   我们将度矩阵（degree matrix） $\mathbf{D}=\text{diag}(d_1,...,d_n)$$\mathbf D=\text{diag}(d_{1}, ..., d_{n})$ 定义为对角矩阵，其中对角线上的每个元素等于邻接矩阵的 row-sum： $d_i=\sum _j{a}_{ij}$$d_{i}=\sum_{j} a_{i j}$ 。

   图中的每个节点 $v_i$$v_{i}$ 都有一个对应的 $d$$d$ 维特征向量 ${\overrightarrow{\mathbf{x}}}_i\in {\mathbb{R}}^d$$\mathbf{\vec x}_{i} \in \mathbb{R}^{d}$ 。整个特征矩阵 $\mathbf{X}\in {\mathbb{R}}^{n\times d}$$\mathbf X \in \mathbb{R}^{n ×d}$ 将 $n$$n$ 个特征向量堆叠在一起， $\mathbf{X}={[{\overrightarrow{\mathbf{x}}}_1,\cdots ,{\overrightarrow{\mathbf{x}}}_n]}^{\mathrm{\top }}$$\mathbf X=\left[\mathbf{\vec x}_{1}, \cdots , \mathbf{\vec x}_{n}\right]^{\top}$ 。每个节点属于 $C$$C$ 个类别中的一个，可以用 $C$$C$ 维 one-hot 向量 ${\overrightarrow{\mathbf{y}}}_i\in \{0,1{\}}^C$$\mathbf{\vec y}_{i} \in \{0,1\}^{C}$ 来表示。我们只知道部分节点的标签，并希望预测 unknown labels。

1.1.1 Graph Convolutional Networks

1. 与 CNN 或 MLP 类似，GCN 通过 multiple layers 为每个节点的特征 ${\overrightarrow{\mathbf{x}}}_i$$\mathbf{\vec x}_{i}$ 学习新的 feature representation，随后将其用作线性分类器的输入。对于第 $k$$k$ 个 graph convolution layer，我们将所有节点的 input node representations 用矩阵 ${\mathbf{H}}^{(k-1)}$$\mathbf H^{(k-1)}$ 来表示，output node representations 用 ${\mathbf{H}}^{(k)}$$\mathbf H^{(k)}$ 来表示。自然地，initial node representations 就是原始输入特征：

   $${\mathbf{H}}^{(0)}=\mathbf{X}$$

   其中 ${\mathbf{H}}^{(0)}$$\mathbf H^{(0)}$ 作为第一个 GCN layer 的输入。

2. 一个 K-layer GCN 等同于对图中每个节点的特征向量 ${\overrightarrow{\mathbf{x}}}_i$$\mathbf{\vec x}_{i}$ 应用一个 K-layer MLP，不同之处在于每个节点的 hidden representation 在每层开始时与其邻居进行平均。在每个 graph convolution layer 中，node representations 通过三个阶段进行更新：feature propagation、linear transformation 和 pointwise nonlinear activation （见 Figure 1 ）。为了清晰起见，我们详细描述每个步骤。

   • 特征传播（Feature propagation）：是 GCN 与 MLP 的区别所在。在每层开始时，每个节点 $v_i$$v_{i}$ 的特征 ${\overrightarrow{\mathbf{h}}}_i$$\mathbf{\vec h}_{i}$ 与其局部邻域中的特征向量进行平均：

     $${\overline{\overrightarrow{\mathbf{h}}}}_i^k\leftarrow \frac{1}{d_i+1}{\overrightarrow{\mathbf{h}}}_i^{(k-1)}+\sum _{j=1}^n\frac{a_{ij}}{\sqrt{(d_i+1)(d_j+1)}}{\overrightarrow{\mathbf{h}}}_j^{(k-1)}$$

     更紧凑地，我们可以将整个图上的这种 update 表示为一个简单的矩阵运算。令 $\mathbf{S}$$\mathbf S$ 表示添加了自环的“归一化”的邻接矩阵：

     $$\mathbf{S}={\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$

     其中：$\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$$\tilde {\mathbf A} = \mathbf A + \mathbf I$，$\mathbf{I}$$\mathbf I$ 为单位矩阵，$\tilde{\mathbf{D}}$$\tilde{\mathbf D}$ 为 $\tilde{\mathbf{A}}$$\tilde{\mathbf A}$ 的 degree matrix 。

     那么，上述公式中对所有节点的同时 update 变为一个简单的稀疏矩阵乘法：

     $${\overline{\mathbf{H}}}^{(k)}\leftarrow \mathbf{S}{\mathbf{H}}^{(k-1)}$$

     直观地说，这一步沿着图的边对 hidden representations 进行局部平滑，并最终促使局部连接的节点之间产生相似的 predictions 。

   • 特征变换和非线性转换（Feature transformation and nonlinear transition）：局部平滑后，GCN layer 等同于标准的MLP 。每层关联一个学到的权重矩阵 ${\mathbf{\Theta }}^{(k)}$$\mathbf{\Theta}^{(k)}$ ，然后对smoothed hidden feature representations 进行线性变换。最后，在输出 feature representation ${\mathbf{H}}^{(k)}$$\mathbf H^{(k)}$ 之前逐点应用非线性激活函数（如 ReLU ）。

     总之，第 $k$$k$ 层的 representation 的更新规则为：

     $${\mathbf{H}}^{(k)}\leftarrow \text{ReLU}\left({\overline{\mathbf{H}}}^{(k)}{\mathbf{\Theta }}^{(k)}\right)$$

     第 $k$$k$ 层的逐点非线性变换之后是第 $(k+1)$$(k+1)$ 层的 featurepropagation 。

   

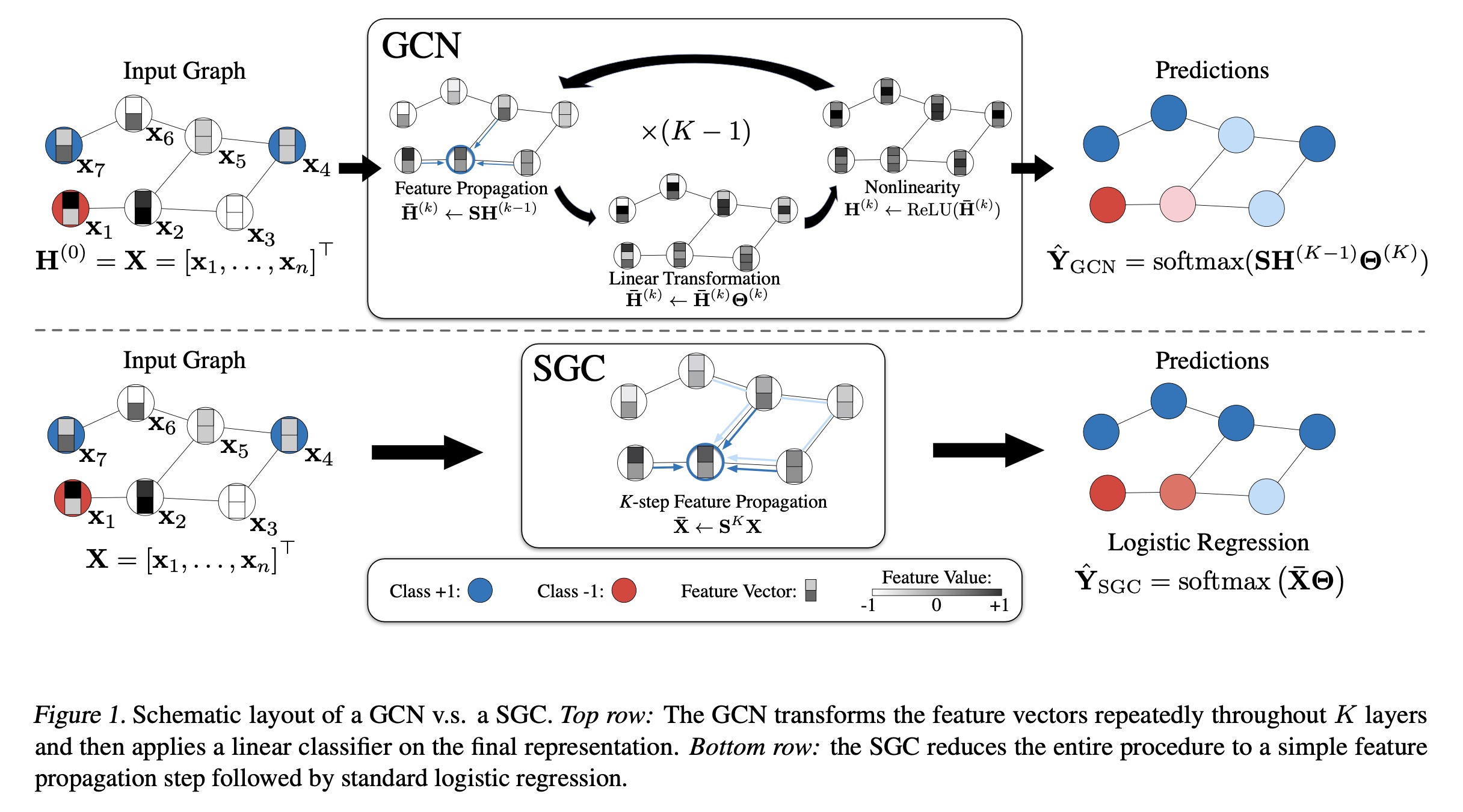
3. 分类器：对于节点分类，与标准 MLP 类似，GCN 的最后一层使用 softmax classifier 来预测 labels 。将 $n$$n$ 个节点的 class predictions 表示为 $\hat{\mathbf{Y}}\in {\mathbb{R}}^{n\times C}$$\hat{\mathbf Y} \in \mathbb{R}^{n ×C}$ ，其中 ${\hat{y}}_{ic}$$\hat{y}_{i c}$ 表示节点 $i$$i$ 属于类别 $c$$c$ 的概率。一个 K-layer GCN 的 class prediction $\hat{\mathbf{Y}}$$\hat{\mathbf Y}$ 可以写成：

   $${\hat{\mathbf{Y}}}_{\text{GCN}}=\text{softmax}\left(\mathbf{S}{\mathbf{H}}^{(K-1)}{\mathbf{\Theta }}^{(K)}\right)$$

   其中： $\text{softmax}(x)=\exp (x)/\sum _{c=1}^C\exp (x_c)$$\text{softmax}(x) = \exp(x) / \sum_{c=1}^{C} \exp(x_{c})$ 作为所有类别上的归一化器。

1.1.2 Simple Graph Convolution

1. 在传统的 MLP 中，deeper layers 通过允许 creation of feature hierarchies 来增加表达能力，例如第二层的特征建立在第一层特征的基础上。在 GCN 中，这些层还有第二个重要功能：在每一层中，hidden representations 在 one hop 邻居之间进行平均。这意味着经过 $k$$k$ 层后，一个节点可以从图中 k−hops 范围内的所有节点获取特征信息。这种效果类似于卷积神经网络，其中深度增加了内部特征的感受野（receptive field）。尽管卷积网络可以从增加的深度中受益匪浅，但通常 MLP 在超过 3 ~ 4 层后获益甚微。

2. 线性化（Linearization ）。我们假设 GCN layers 之间的非线性并非关键——但大部分好处来自局部平均（local averaging）。因此，我们移除各层之间的非线性转换函数，仅保留 final softmax（以获得概率性的输出）。所得模型是线性的，但仍然具有 K-layer GCN 相同的 increased 的“感受野”：

   $$\hat{\mathbf{Y}}=\text{softmax}(\mathbf{S}\cdots \mathbf{S}\mathbf{S}\mathbf{X}{\mathbf{\Theta }}^{(1)}{\mathbf{\Theta }}^{(2)}\cdots {\mathbf{\Theta }}^{(K)})$$

   为了简化符号，我们可以将与归一化的邻接矩阵（normalized adjacency matrix ） $\mathbf{S}$$\mathbf S$ 的重复乘法合并为一个单一矩阵，即 $\mathbf{S}$$\mathbf S$ 的 $K$$K$ 次幂 ${\mathbf{S}}^K$$\mathbf S^{K}$ 。此外，我们可以将权重重新参数化为单个矩阵 $\mathbf{\Theta }={\mathbf{\Theta }}^{(1)}{\mathbf{\Theta }}^{(2)}\cdots {\mathbf{\Theta }}^{(K)}$$\mathbf \Theta = \mathbf \Theta^{(1)} \mathbf \Theta^{(2)} \cdots \mathbf \Theta^{(K)}$ 。所得的分类器变为：

   $${\hat{\mathbf{Y}}}_{\text{GCN}}=\text{softmax}\left({\mathbf{S}}^K\mathbf{X}\mathbf{\Theta }\right)$$

   我们将其称为 Simple Graph Convolution: SGC。

3. 逻辑回归（Logistic regression）：上式为 SGC 提供了自然且直观的解释。通过区分 feature extraction 和 classifier，SGC 由两部分组成：

   • 固定的（即无参数的）feature extraction/smoothing 组件： $\overline{\mathbf{X}}={\mathbf{S}}^K\mathbf{X}$$\bar{\mathbf X} = \mathbf S^K\mathbf X$ 。

   • 跟线性逻辑回归分类器： $\hat{\mathbf{Y}}=\text{softmax}(\overline{\mathbf{X}}\mathbf{\Theta })$$\hat{\mathbf Y} = \text{softmax}(\bar{\mathbf X} \mathbf \Theta)$ 。

   由于 $\overline{\mathbf{X}}$$\bar{\mathbf X}$ 的计算不需要权重，它本质上等同于特征预处理（feature pre-processing）步骤，并且模型的整个训练简化为对预处理后的特征 $\overline{\mathbf{X}}$$\bar{\mathbf X}$ 进行直接的多类逻辑回归（multi-class logistic regression）。

4. Optimization细节：逻辑回归的训练是一个经过充分研究的凸优化问题，可以使用任何高效的二阶方法或随机梯度下降（《Large-scale machine learning with stochastic gradient descent》）进行。假设 graph connectivity pattern 足够稀疏，SGD自然可以扩展到非常大的图规模，并且 SGC 的训练速度比 GCN 快得多。

1.2 频谱分析

1. 我们现在从 graph convolution 的角度研究 SGC。我们证明 SGC 对应于图频谱域（graph spectral domain ）上的一个固定滤波器（fixed filter）。此外，我们表明向原始图添加自环（即 renormalization trick ）可有效缩小 underlying graph spectrum。在这个 scaled domain 上，SGC 充当低通滤波器（low-pass filter），在图上生成平滑的特征（smooth features）。因此，邻近节点往往具有相似的 representations，从而产生相似的 predictions。

1.2.1 图卷积预备知识

1. 与欧几里得域类似，图傅里叶分析（graph Fourier analysis）依赖于图拉普拉斯矩阵（graph Laplacians）的谱分解（spectral decomposition）。图拉普拉斯矩阵 $\mathbf{\Delta }=\mathbf{D}-\mathbf{A}$$\mathbf\Delta = \mathbf D - \mathbf A$ （及其归一化版本 ${\mathbf{\Delta }}_{\text{sym}}={\mathbf{D}}^{-1/2}\mathbf{\Delta }{\mathbf{D}}^{-1/2}$$\mathbf\Delta_{\text{sym}} = \mathbf D^{-1/2}\mathbf \Delta\mathbf D^{-1/2}$ ）是对称半正定矩阵，具有特征分解（eigendecomposition） ：

   $$\mathbf{\Delta }=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\mathrm{\top }}$$

   其中：

   • $\mathbf{U}\in {\mathbb{R}}^{n\times n}$$\mathbf U \in \mathbb{R}^{n \times n}$ 由标准正交特征向量组成。

   • $\mathbf{\Lambda }=\text{diag}({\lambda }_1,\dots ,{\lambda }_n)$$\mathbf \Lambda = \text{diag}(\lambda_1, \dots, \lambda_n)$ 是特征值组成的对角矩阵。

   拉普拉斯矩阵的特征分解使我们能够在 graph domain 上定义等效的傅里叶变换，其中特征向量表示傅里叶模式（Fourier modes ），特征值表示图的频率。在此框架下，设 $\overrightarrow{\mathbf{x}}\in {\mathbb{R}}^n$$\mathbf{\vec x} \in \mathbb{R}^n$ 为定义在图顶点上的信号。我们将 $\overrightarrow{\mathbf{x}}$$\mathbf{\vec x}$ 的图傅里叶变换定义为 $\widehat{\overrightarrow{\mathbf{x}}}={\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{x}}$$\hat{\mathbf {\vec x}} = \mathbf U^{\top} \mathbf{\vec x}$ ，其逆运算为 $\overrightarrow{\mathbf{x}}=\mathbf{U}\widehat{\overrightarrow{\mathbf{x}}}$$\mathbf{\vec x} = \mathbf U \hat{\mathbf{\vec x}}$ 。因此，信号 $\overrightarrow{\mathbf{x}}$$\mathbf{\vec x}$ 与滤波器 $\overrightarrow{\mathbf{g}}$$\mathbf {\vec g}$ 之间的 graph convolution 运算为：

   $$\overrightarrow{\mathbf{g}}\ast \overrightarrow{\mathbf{x}}=\mathbf{U}(\left({\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{g}}\right)\odot \left({\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{x}}\right))=\mathbf{U}\hat{\mathbf{G}}{\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{x}}$$

   其中： $\hat{\mathbf{G}}=\text{diag}({\hat{g}}_1,\dots ,{\hat{g}}_n)$$\hat{\mathbf G} = \text{diag}\left(\hat{g}_1, \dots, \hat{g}_n\right)$ 表示对角矩阵，其对角线对应 spectral filter 的系数。

   注意：$(g_1,\cdots ,g_n)$$(g_1,\cdots,g_n)$ 是在频域中的；而 $({\hat{g}}_1,\dots ,{\hat{g}}_n)$$\left(\hat{g}_1, \dots, \hat{g}_n\right)$ 是在谱域中的。

2. Graph convolutions 可以用拉普拉斯矩阵的 $k$$k$ 阶多项式近似：

   $$\mathbf{U}\hat{\mathbf{G}}{\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{x}}\simeq \sum _{i=0}^k{\theta }_i{\mathbf{\Lambda }}^i\overrightarrow{\mathbf{x}}=\mathbf{U}\left(\sum _{i=0}^k{\theta }_i{\mathbf{\Lambda }}^i\right){\mathbf{U}}^{\mathrm{\top }}\overrightarrow{\mathbf{x}}$$

   其中 ${\theta }_i$$\theta_i$ 表示系数。

   在这种情况下，滤波器系数对应于拉普拉斯特征值的多项式，即 $\hat{\mathbf{G}}=\sum _i{\theta }_i{\mathbf{\Lambda }}^i$$\hat{\mathbf G} = \sum_i \theta_i \mathbf \Lambda^i$ ，或等价地 $\hat{g}({\lambda }_j)=\sum _i{\theta }_i{\lambda }_j^i$$\hat{g}(\lambda_j) = \sum_i \theta_i \lambda_j^i$ 。

   图卷积网络（ 《Semi-supervised classification with graph convolutional networks》 ）采用 $k=1$$k=1$ 时的仿射近似，系数为 ${\theta }_0=2\theta$$\theta_0 = 2\theta$ 和 ${\theta }_1=-\theta$$\theta_1 = -\theta$ ，由此得到基本的 GCN 卷积运算：

   $$\overrightarrow{\mathbf{g}}\ast \overrightarrow{\mathbf{x}}=\theta (\mathbf{I}+{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2})\overrightarrow{\mathbf{x}}$$

   在最终设计中，《Semi-supervised classification with graph convolutional networks》 将矩阵 $\mathbf{I}+{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\mathbf I + \mathbf D^{-1/2}\mathbf A \mathbf D^{-1/2}$ 替换为归一化版本 ${\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$\tilde{\mathbf D}^{-1/2} \tilde{\mathbf A} \tilde{\mathbf D}^{-1/2}$ ，其中 $\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$$\tilde{\mathbf A} = \mathbf A +\mathbf I$ ，相应地 $\tilde{\mathbf{D}}=\mathbf{D}+\mathbf{I}$$\tilde{\mathbf D} = \mathbf D + \mathbf I$ ，这被称为重新归一化技巧（renormalization trick）。

   最后，通过将卷积推广到处理 d-channel input 中的多个滤波器，并在每层之间使用非线性激活函数，我们得到了 GCN 传播规则。

1.2.2 SGC与低通滤波

1. GCN 中推导的初始的一阶切比雪夫滤波器对应于 propagation matrix ${\mathbf{S}}_{\text{1-order}}=\mathbf{I}+{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\mathbf S_{\text{1-order}} = \mathbf I + \mathbf D^{-1/2} \mathbf A \mathbf D^{-1/2}$ 。由于归一化的拉普拉斯矩阵为 ${\mathbf{\Delta }}_{\text{sym}}=\mathbf{I}-{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\mathbf \Delta_{\text{sym}} = \mathbf I - \mathbf D^{-1/2} \mathbf A \mathbf D^{-1/2}$ ，因此 ${\mathbf{S}}_{\text{1-order}}=2\mathbf{I}-{\mathbf{\Delta }}_{\text{sym}}$$\mathbf S_{\text{1-order}} = 2\mathbf I - \mathbf \Delta_{\text{sym}}$ 。因此，使用 ${\mathbf{S}}_{\text{1-order}}^K$$\mathbf S_{\text{1-order}}^K$ 进行 feature propagation 意味着滤波器系数 ${\hat{g}}_i=\hat{g}({\lambda }_i)=(2-{\lambda }_i{)}^K$$\hat{g}_i = \hat{g}(\lambda_i) = (2 - \lambda_i)^K$ ，其中 ${\lambda }_i$$\lambda_i$ 表示 ${\mathbf{\Delta }}_{\text{sym}}$$\mathbf \Delta_{\text{sym}}$ 的特征值。Figure 2 展示了与 ${\mathbf{S}}_{\text{1-order}}$$\mathbf S_{\text{1-order}}$ 相关的滤波操作，其中传播步数 $K\in \{1,\dots ,6\}$$K \in \{1, \dots, 6\}$ 不同。可以观察到， ${\mathbf{S}}_{\text{1-order}}$$\mathbf S_{\text{1-order}}$ 的高次幂会导致滤波器系数爆炸，并不必要地过度放大频率 ${\lambda }_i<1$$\lambda_i < 1$ 的信号。

   为解决一阶切比雪夫滤波器可能存在的数值问题， 《Semi-supervised classification with graph convolutional networks》 提出了 renormalization trick。本质上，它包括将 ${\mathbf{S}}_{\text{1-order}}$$\mathbf S_{\text{1-order}}$ 替换为添加所有节点自环后的归一化的邻接矩阵。我们将所得的 propagation 矩阵称为 augmented normalized adjacency matrix ${\tilde{\mathbf{S}}}_{\text{adj}}={\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$\tilde{\mathbf S}_{\text{adj}} = \tilde{\mathbf D}^{-1/2} \tilde{\mathbf A} \tilde{\mathbf D}^{-1/2}$ ，其中 $\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}$$\tilde{\mathbf A} =\mathbf A + \mathbf I$ ， $\tilde{\mathbf{D}}=\mathbf{D}+\mathbf{I}$$\tilde{\mathbf D} =\mathbf D +\mathbf I$ 。相应地，我们定义 augmented normalized Laplacian ${\tilde{\mathbf{\Delta }}}_{\text{sym}}=\mathbf{I}-{\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$\tilde{\mathbf \Delta}_{\text{sym}} = \mathbf I - \tilde{\mathbf D}^{-1/2} \tilde{\mathbf A} \tilde{\mathbf D}^{-1/2}$ 。因此，我们可以将与 ${\tilde{\mathbf{S}}}_{\text{adj}}$$\tilde{\mathbf S}_{\text{adj}}$ 相关的频谱滤波器描述为底层拉普拉斯矩阵特征值的多项式，即 $\hat{g}({\tilde{\lambda }}_i)=(1-{\tilde{\lambda }}_i{)}^K$$\hat{g}(\tilde{\lambda}_i) = (1 - \tilde{\lambda}_i)^K$ ，其中 ${\tilde{\lambda }}_i$$\tilde{\lambda}_i$ 是 ${\tilde{\mathbf{\Delta }}}_{\text{sym}}$$\tilde{\mathbf \Delta}_{\text{sym}}$ 的特征值。

   我们现在分析 ${\tilde{\mathbf{\Delta }}}_{\text{sym}}$$\tilde{\mathbf \Delta}_{\text{sym}}$ 的频谱，并表明向图中添加自环会缩小相应 normalized Laplacian 的频谱（特征值）。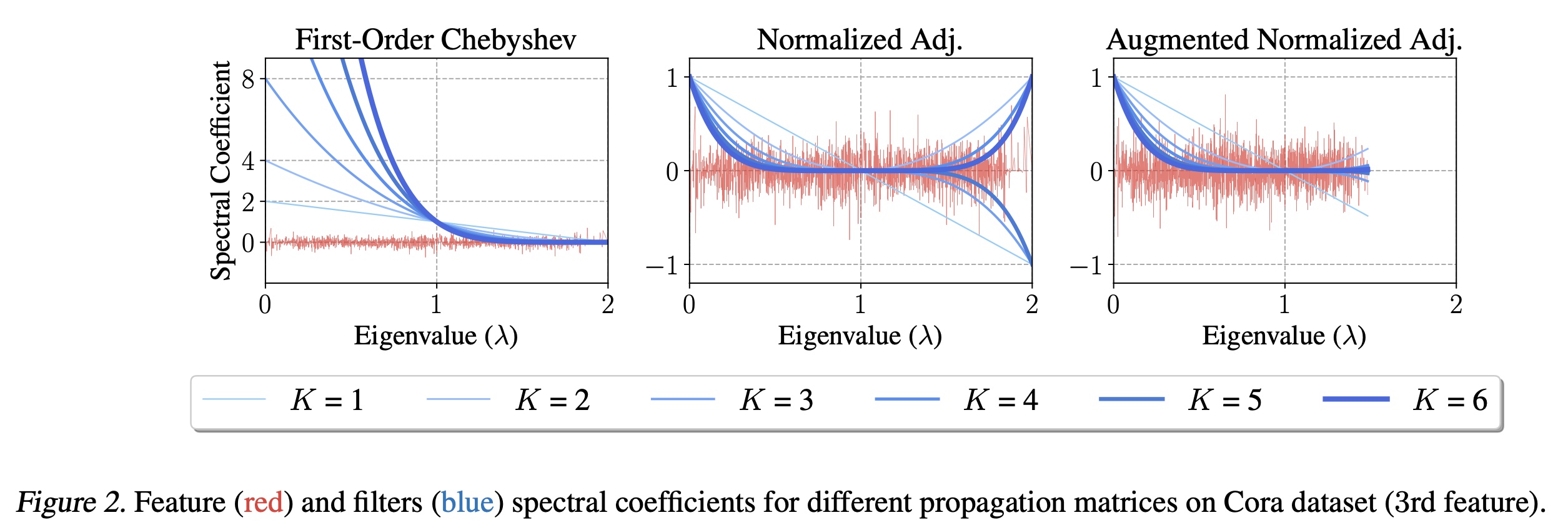

   

2. 定理 1 ：设 $\mathbf{A}$$\mathbf A$ 为无向、加权、简单图 $\mathcal{G}$$\mathcal G$ 的邻接矩阵，图中无孤立节点，对应度矩阵为 $\mathbf{D}$$\mathbf D$ 。设 $\tilde{\mathbf{A}}=\mathbf{A}+\gamma \mathbf{I}$$\tilde{\mathbf A} = \mathbf A + \gamma \mathbf I$ （ $\gamma >0$$\gamma > 0$ ）为 augmented adjacency matrix，对应度矩阵为 $\tilde{\mathbf{D}}$$\tilde{\mathbf D}$ 。令 ${\lambda }_1$$\lambda_1$ 和 ${\lambda }_n$$\lambda_n$ 分别表示 ${\mathbf{\Delta }}_{\text{sym}}=\mathbf{I}-{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\mathbf \Delta_{\text{sym}} = \mathbf I -\mathbf D^{-1/2} \mathbf A \mathbf D^{-1/2}$ 的最小特征值和最大特征值；类似地，令 ${\tilde{\lambda }}_1$$\tilde{\lambda}_1$ 和 ${\tilde{\lambda }}_n$$\tilde{\lambda}_n$ 为 ${\tilde{\mathbf{\Delta }}}_{\text{sym}}=\mathbf{I}-{\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$\tilde{\mathbf \Delta}_{\text{sym}} = \mathbf I - \tilde{\mathbf D}^{-1/2} \tilde{\mathbf A} \tilde{\mathbf D}^{-1/2}$ 的最小特征值和最大特征值。我们有：

   $$0={\lambda }_1={\tilde{\lambda }}_1<{\tilde{\lambda }}_n<{\lambda }_n$$

   定理 1 表明，添加自环（ $\gamma >0$$\gamma > 0$ ）后，normalized graph Laplacian 的最大特征值变小（证明见补充材料）。

3. Figure 2 描绘了 Cora 数据集上 normalized adjacency ${\mathbf{S}}_{\text{adj}}={\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$$\mathbf S_{\text{adj}} = \mathbf D^{-1/2}\mathbf A \mathbf D^{-1/2}$ 及其增强的变体 ${\tilde{\mathbf{S}}}_{\text{adj}}={\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}$$\tilde{\mathbf S}_{\text{adj}} = \tilde{\mathbf D}^{-1/2} \tilde{\mathbf A} \tilde{\mathbf D}^{-1/2}$ 的滤波操作。使用 ${\mathbf{S}}_{\text{adj}}$$\mathbf S_{\text{adj}}$ 进行 feature propagation对应于频谱范围 $[0,2]$$[0, 2]$ 内的滤波器 $g({\lambda }_i)=(1-{\lambda }_i{)}^K$$g(\lambda_i) = (1 - \lambda_i)^K$ ；因此， ${\mathbf{S}}_{\text{adj}}$$\mathbf S_{\text{adj}}$ 的奇数次幂会在频率 ${\lambda }_i>1$$\lambda_i > 1$ 处产生负滤波器系数。通过添加自环（ ${\tilde{\mathbf{S}}}_{\text{adj}}$$\tilde{\mathbf S}_{\text{adj}}$ ），最大特征值从 2 缩小到约 1.5，从而消除了负系数的影响。

   此外，这种缩放后的频谱允许取 ${\tilde{\mathbf{S}}}_{\text{adj}}$$\tilde{\mathbf S}_{\text{adj}}$ 的 $K>1$$K > 1$ 次幂所定义的滤波器充当低通型滤波器。在补充材料中，我们对 propagation matrix 的不同选择进行了实证评估。

1.3 实验

1. 我们首先在引文网络和社交网络上评估 SGC ，然后将实证分析扩展到广泛的下游任务。

1.3.1 引文网络与社交网络

1. 我们在 Cora、Citeseer 和 Pubmed 引文网络数据集（Table 2 ）上评估 SGC 的半监督节点分类性能。通过使用 SGC 对 Reddit （Table 3）的社区结构进行归纳性的预测来补充引文网络分析，Reddit 包含更大的图。数据集统计信息汇总在 Table 1 中。

   

2. 数据集与实验设置：

   • 在引文网络上，我们使用 Adam 训练 SGC 达 100 个 epoch，学习率为 0.2。此外，我们使用 weight decay ，并通过 hyperopt 在公开的 split validation set 上进行 60 次迭代从而调优每个数据集的超参数。引文网络实验以直推式（transductively ）进行。

   • 在 Reddit 数据集上，我们使用 L-BFGS 训练 SGC，不使用正则化，且训练在 2 steps 内收敛。我们按照 《FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling》 的方法进行归纳式（inductively）评估：在仅包含训练节点的子图上训练 SGC ，并在原始图上测试。

   在所有数据集上，我们根据收敛行为和验证准确来调优 epoch 数。

3. baseline：

   • 对于引文网络，我们将 SGC 与 GCN、GAT、FastGCN、LNet、AdaLNet 和 DGI 进行比较。其中这些基线模型都采用公开实现的版本。由于 GIN 最初未在引文网络上评估，我们按照 《How powerful are graph neural networks?》 来实现 GIN，并使用 hyperopt 在 60 iterations 内调优 weight decay 和学习率。此外，我们手动调优 hidden dimension 。

   • 对于 Reddit，我们将 SGC 与 GaAN、GraphSAGE 的监督和无监督变体、FastGCN 和 DGI 的报告性能进行比较。Table 3 还突出显示了每种方法的 feature extraction step 的设置。值得注意的是，SGC 不涉及学习，因为 eature extraction step ${\mathbf{S}}^K\mathbf{X}$$\mathbf S^K \mathbf X$ 没有参数。无监督方法和 no-learning 方法均在之后使用 labels 来训练逻辑回归模型。

4. 性能：根据 Table 2 和 Table 3 的结果，我们得出 SGC 具有很强竞争力的结论。

   Table 2 显示：

   • SGC 在引文网络上的性能可与GCN 和 SOTA 的图网络相媲美。特别是在 Citeseer 上，SGC 比 GCN 高约 1% ，我们认为这种性能提升是由于 SGC 参数更少，因此过拟合更少。

   • 值得注意的是，GIN 由于过拟合表现稍差。

   • 此外，LNet 和 AdaLNet 在引文网络上不稳定。

   在 Reddit 上，Table 3 显示 SGC 比之前的基于采样的 GCN 变体（SAGE-GCN 和 FastGCN ）高出 1% 以上。

   值得注意的是，《Deep Graph InfoMax》 报告称，随机初始化的 DGI encoder 的性能几乎与 trained encoder 相当；然而，这两种模型在 Reddit 上的表现均不如 SGC。这一结果可能表明，DGI encoder 中的额外权重和非线性即使不是完全有害的，也是多余的。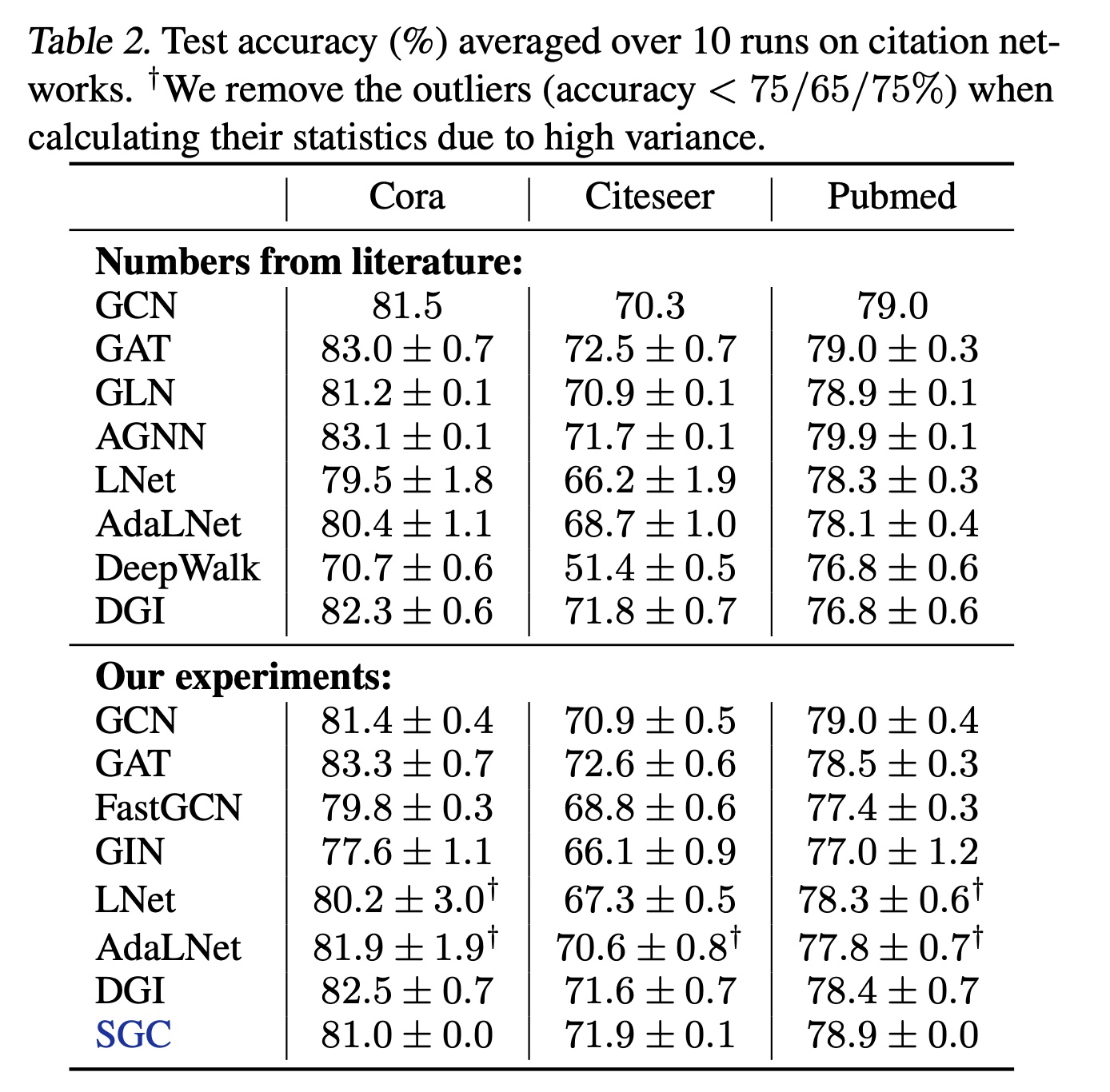

   

   

5. 效率：在 Figure 3 中，我们绘制了 SOTA 的图网络在 Pubmed 数据集和 Reddit 数据集上的性能、以及它们其相对于 SGC 的训练时间的关系。特别地，我们预计算 ${\mathbf{S}}^K\mathbf{X}$$\mathbf S^K \mathbf X$ ，SGC 的训练时间考虑了此 precomputation 时间。我们在 NVIDIA GTX 1080 Ti GPU 上测量训练时间，基准细节见补充材料。

   在大型图（如 Reddit ）上，由于内存需求过高，GCN 无法训练。先前的方法通过采样减少邻域大小（FastGCN 、GraphSage）或限制模型大小（DGI ）来解决这一限制。通过应用固定滤波器并预计算 ${\mathbf{S}}^K\mathbf{X}$$\mathbf S^K \mathbf X$ ，SGC 最小化内存使用，仅在训练期间学习单个权重矩阵。由于 $\mathbf{S}$$\mathbf S$ 通常是稀疏的且 $K$$K$ 通常较小，我们可以利用快速 sparse-dense 矩阵乘法来计算 ${\mathbf{S}}^K\mathbf{X}$$\mathbf S^K \mathbf X$ 。Figure 3 显示，SGC 的训练速度比基于快速采样的方法快两个数量级，同时性能几乎没有下降。

   

1.3.2 下游任务

1. 我们将实证评估扩展到 5 个下游应用以研究 SGC 的适用性：文本分类、半监督的用户地理定位、关系抽取、zero-shot 图像分类、以及 graph 分类。实验设置见补充材料。

2. 文本分类（Text classification）：为文档分配标签。《Graph convolutional networks for text classification》 使用两层 GCN，将文档和单词均视为图中节点，从而实现了 SOTA 的结果。word-word 的边权重为 pointwise mutual information: PMI，word-document的边权重为归一化的 TF-IDF 分数。Table 4 显示，SGC（ $K=2$$K=2$ ）在 5 个基准数据集上与他们的模型相当，同时快达 83.6 倍。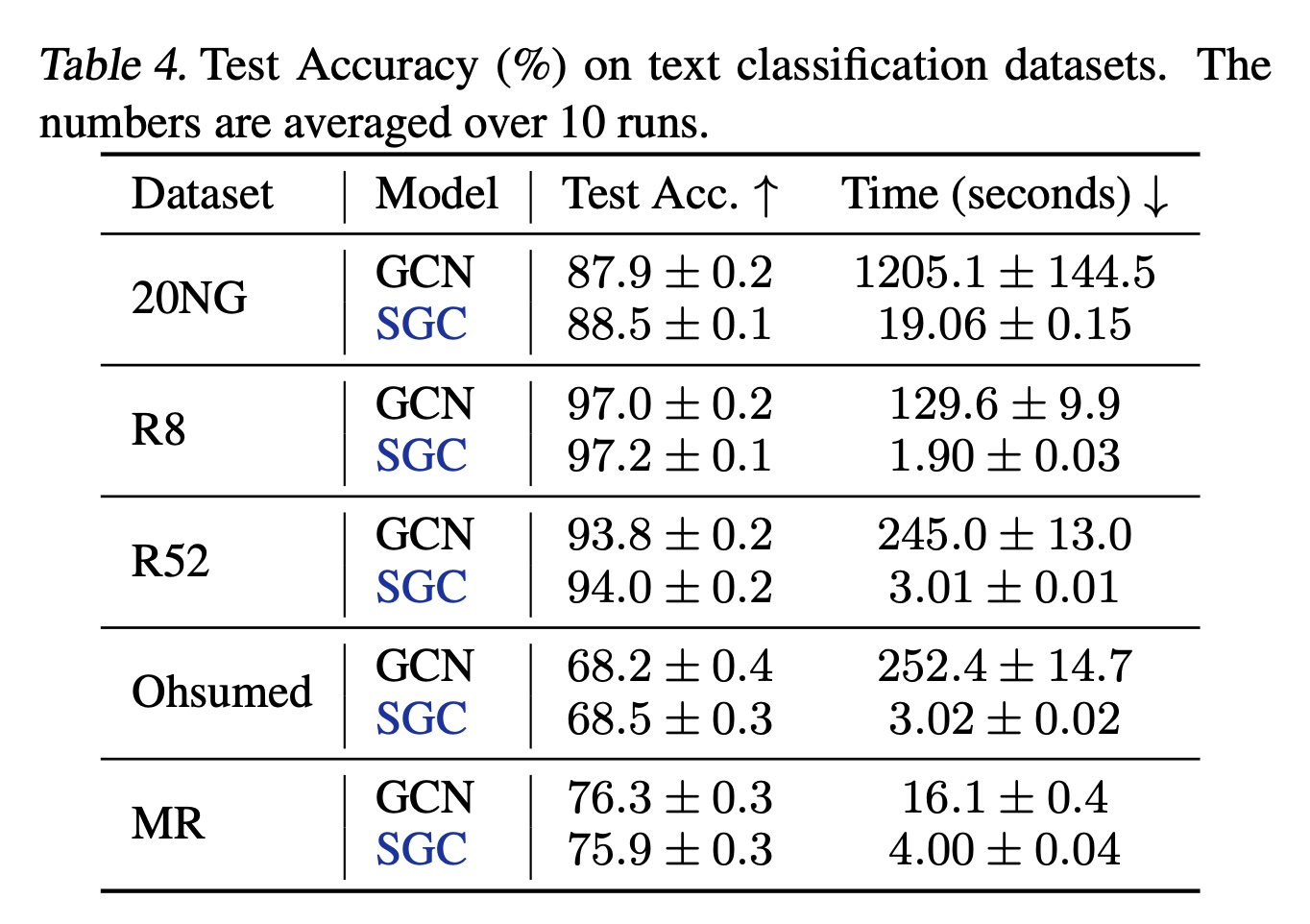

   

3. 半监督用户地理定位（Semi-supervised user geolocation）：根据用户的帖子、用户之间的连接、以及少量标记用户，定位社交媒体上用户的 “home” position 。 《Semi-supervised user geolocation via graph convolutional networks》在此任务上应GCNs with highway connections，取得了接近 SOTA 的结果。Table 5 显示，在 《Semi-supervised user geolocation via graph convolutional networks》在的框架下，SGC 在 GEOTEXT、TWITTER-US 和 TWITTER-WORLD 上优于 GCN with highway con- nections ，同时在 TWITTER-WORLD 上节省了 30 多个小时。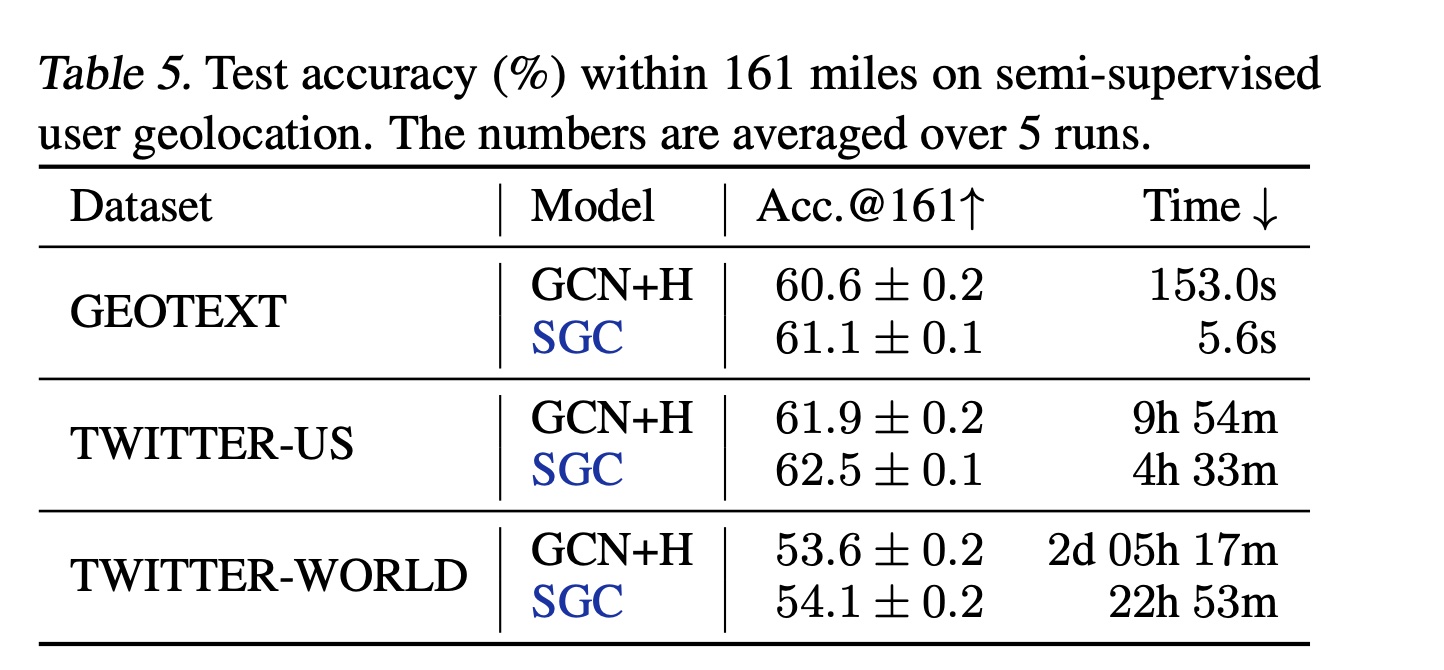

   

4. 关系抽取（Relation extraction）：涉及预测句子中主语和宾语之间的关系。《Graph convolution over pruned dependency trees improves relation extraction》提出 C-GCN，其使用LSTM 后跟 GCN 和 MLP 。我们将 GCN 替换为 SGC（ $K=2$$K=2$ ），并将所得模型称为 C-SGC。Table 6 显示，C-SGC 在 TACRED 上创下新的 SOTA 。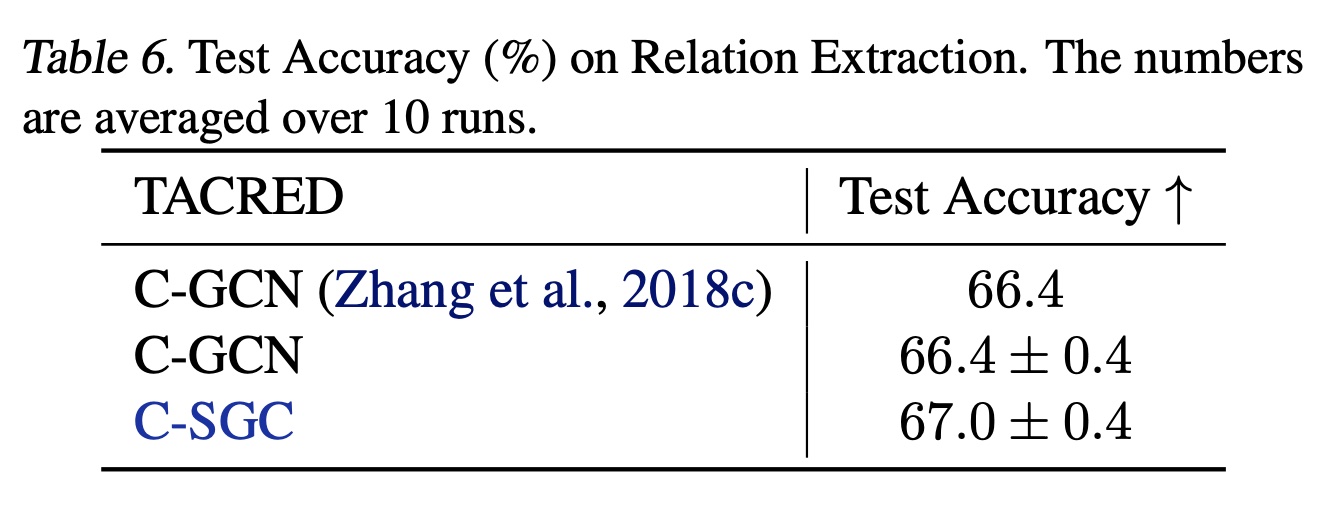

   

5. 零样本图像分类（Zero-shot image classification）：无法访问 test categories 中任何图像或者 label 的情况下，学习一个图像分类器。GCNZ 使用 GCN 根据 WordNet 中的关系将 category names 映射到 image feature domain ，并找到与 query image feature vector 最相似的类别。Table 7 显示，将 GCN 替换为 MLP 后跟 SGC 可提高性能，同时将参数数量减少 55%。我们发现，MLP feature extractor 对于将 pretrained GloVe vectors 映射到 ResNet-50 提取的视觉特征空间是必要的。同样，这一下游应用表明，学到的 graph convolution filters 是多余的；类似于 《Classifier and exemplar synthesis for zero-shot learning》 的观察，即 GCN 可能并非必要。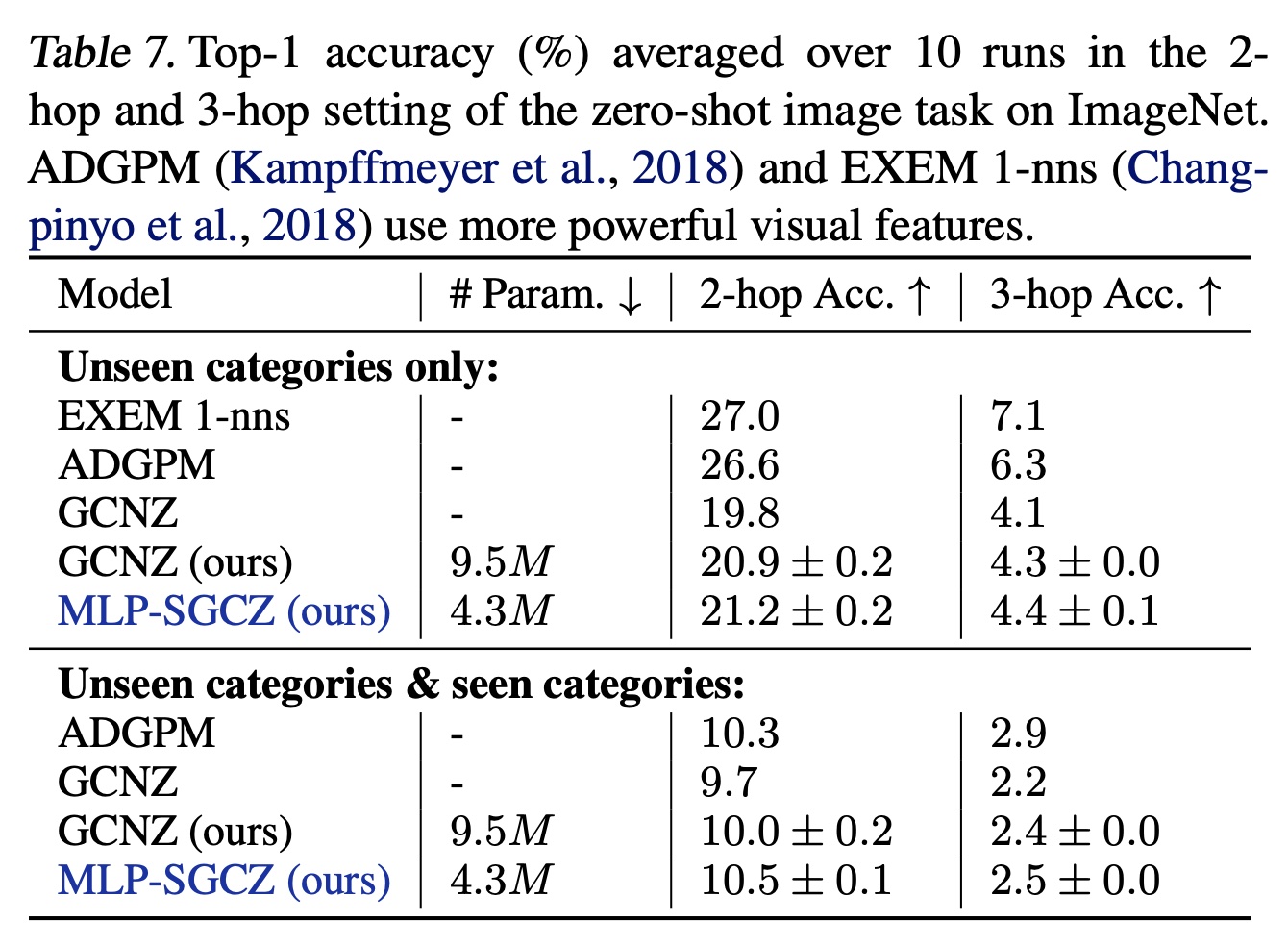

   

6. 图分类（Graph classification）：要求模型使用 graph structure 对 graph 进行分类。《How powerful are graph neural networks?》 从理论上表明，GCN 不足以区分某些图结构，并表明他们的 GIN 更具表达能力，在各种图分类数据集上取得了 SOTA 的结果。我们将 DCGCN 中的 GCN 替换为 SGC，在 NCI1 和 COLLAB 数据集上分别获得 71.0% 和 76.2% 的准确率，与 GCN 相当，但远低于 GIN 。类似地，在 QM8 量子化学数据集上，更先进的 AdaLNet 和 LNet 在 QM8 上的 MAE 为 0.01，显著优于 SGC 的0.03 的 MAE。

1.4 结论

1. 为了更好地理解和解释 GCN 的机制，我们探索了图卷积模型的最简单可能形式——SGC 。该算法几乎是 trivial的：一个基于图的预处理步骤，随后接标准的多类逻辑回归。然而，SGC 的性能在广泛的图学习任务中与 GCN 和 SOTA 的图神经网络模型相当，甚至更优。此外，通过预计算固定的特征提取器 ${\mathbf{S}}^K$$\mathbf S^K$ ，训练时间大幅降低。例如，在 Reddit 数据集上，SGC 的训练速度比基于采样的 GCN 变体快两个数量级。

   除了实证分析，我们还从卷积角度分析了 SGC，证明其在频谱域上相当于一个低通型滤波器。低通型滤波器捕获低频信号，这对应于在图上 smoothing features 。我们的分析还解释了 renormalization trick 的实证效果，表明缩小频谱域如何产生支撑 SGC 的低通型滤波器。

   最终，SGC 的优异性能揭示了 GCN 的本质：其表达能力很可能主要来自于 repeated graph propagation （SGC保留了这一点），而非 nonlinear feature extraction （SGC未采用）。

   鉴于其实证性能、效率和可解释性，我们认为 SGC 至少在三个方面对社区具有重要价值：

   • (1)：作为首选模型，尤其是节点分类任务。

   • (2)：作为与未来 graph learning models 比较的简单基线。

   • (3)：作为 graph learning 未来研究的起点——回归机器学习从简单模型发展为复杂模型的历史实践。